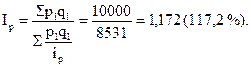|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Средние арифметические и средние гармонические индексы
Основной формой общих индексов является агрегатный, представляющий собой отношение агрегатов, т.е. соединений различных (однородных и неоднородных) элементов сложного показателя, приведенного к сопоставимому виду. Числитель этого индекса рассчитывают как сумму произведений индексируемой величины отчетного периода на веса (соизмерители). Знаменатель агрегатного индекса находят как сумму произведений индексируемой величины базисного периода на те же веса (соизмерители). При построении агрегатных индексов значение придается объективному выбору весов (соизмерителей) и того периода, к которому они должны относиться. Поэтому не будет излишним подчеркнуть, что агрегатные индексы количественных (объемных) признаков практически строятся с весами (соизмерителями), относящимися к базисному периоду, а индексы качественных признаков – с весами (соизмерителями) отчетного периода. Выбор формы агрегатного индекса непосредственно зависит от наличия исходной информации. Если эта она представляет собой полное сочетание абсолютных данных о количественных и качественных признаках за сравниваемые периоды или по территориальным объектам, то можно воспользоваться стандартными формулами расчета агрегатных индексов. Так, для расчета общего индекса физического объема товаров стандартную формулу обычно записывают так:
Общий индекс цен на товары выглядит следующим образом:
Однако в ряде случаев для расчета общих индексов исходная информация может носить видоизмененный характер. Например, вместо количества товаров, цен в базисном или отчетном периодах имеются индивидуальные индексы, либо коэффициенты роста (прироста) физического объема, цен. В такой ситуации стандартные формулы общих индексов могут быть преобразованы в средние арифметические или гармонические. Проведем теоретические преобразования стандартных агрегатных индексов в средние на примере общих индексов прежде всего физического объема товаров. Из формулы (10.3) индивидуального индекса физического объема следует, что
Допустим, организация по переработке овощей и фруктов продала консервированную продукцию за два периода. Фактические результаты реализации и вспомогательные расчеты приведены в табл. 10.3.
Т а б л и ц а 10.3. Динамика реализации консервированной продукции
Необходимо найти общий индекс физического объема, т.е. определить, как изменилась стоимость проданной продукции за счет ее физического объема. Данные, полученные в табл. 10.3, подставим в (10.11):
Найденный общий индекс показывает, что в перерабатывающей организации стоимость проданной консервированной продукции в отчетном периоде по сравнению с базисным увеличилась в 1,054 раза (на 5,4 %) за счет динамики (изменения) физического объема (количества) продукции. Если в стандартную формулу (10.9) вместо q0 подставить
Для примера воспользуемся данными опять-таки о реализации продукции в организации по переработке овощей и фруктов (табл. 10.4), где приведены не только фактические результаты продажи, но и вспомогательные расчеты. Необходимо найти общий индекс физического объема и оценить, как изменилась стоимость товарной продукции за счет ее физического объема. Подставим данные табл. 10.4 в формулу (10.12) и получим:
Т а б л и ц а 10.4. Динамика товарной продукции перерабатывающей Организации
Средний гармонический индекс физического объема (1,054) – это не простое совпадение со средним арифметическим индексом, а свидетельство того, что к одному и тому же результату можно прийти различными приемами. При преобразовании стандартной формулы (10.10) общего индекса цен в средней арифметический индекс необходимо иметь в виду, что индивидуальный индекс цен
Если же в знаменателе стандартной формулы (10.10) агрегатного индекса базисные цены р0 заменить на равнозначные им отношения
Для закрепления теоретических положений по применению среднего гармонического индекса цен воспользуемся примером. Допустим, сельскохозяйственная организация «Днепр» реализовала продукцию животноводства в первом и втором кварталах календарного года (табл. 10.5). Необходимо определить, как изменилась стоимость продукции во втором квартале по сравнению с первым за счет реализованных цен. Данные табл. 10.5 позволяют рассчитать средний гармонический индекс цен (по формуле 10.13):
Т а б л и ц а 10.5. Динамика реализации животноводческой продукции в сельхозорганизации «Днепр»
Следовательно, стоимость проданной продукции животноводства во втором квартале по сравнению с первым за счет цен реализации возросла в 1,172 раза, или на 17,2 %.
Дата добавления: 2016-06-06 | Просмотры: 667 | Нарушение авторских прав |
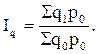 (10.9)
(10.9) (10.10)
(10.10) а
а  . Подставим в числитель агрегатного индекса физического объема (формула 10.9) вместо отчетного количества q1 равнозначные ему произведения iqq0 и получим средний арифметический индекс физического объема:
. Подставим в числитель агрегатного индекса физического объема (формула 10.9) вместо отчетного количества q1 равнозначные ему произведения iqq0 и получим средний арифметический индекс физического объема: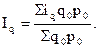 (10.11)
(10.11)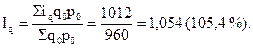
 , то получим средний гармонический индекс физического объема:
, то получим средний гармонический индекс физического объема: . (10.12)
. (10.12)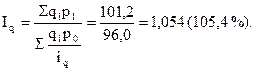

 Заменив в числителе стандартного агрегатного индекса (10.10) цены отчетного периода р1 на ipp0, получим средний арифметический индекс цен:
Заменив в числителе стандартного агрегатного индекса (10.10) цены отчетного периода р1 на ipp0, получим средний арифметический индекс цен: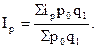 (10.13)
(10.13) то получим средний гармонический индекс цен:
то получим средний гармонический индекс цен: (10.14)
(10.14)