 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Понятие о простейших показателях вариации
Выше отмечалось, что вариация – это колеблемость, изменение величины признака в статистической совокупности, т.е. принятие единицами совокупности разных значений признака. Например, колебания урожайности ржи в фермерских хозяйствах, зарплаты у работников льноперерабатывающей организации и т.д. Измерение вариации позволяет определить степень воздействия на изучаемый признак других варьирующих признаков, установить, например, какие факторы и в какой степени влияют на урожайность ржи, на размер зарплаты работников и т.д. Простейший показатель вариации признака – вариационный размах. Вариационный размах (амплитуда колебаний) признака рассчитывается как разность между максимальной и минимальной вариантами определённого количественного признака в статистической совокупности:
где Rх – размах вариации признака; Так, например, если живая масса одной головы в стаде молодняка крупного рогатого скота колеблется в пределах от 200 до 350 кг, то вариационный размах по живой массе молодняка составляет 150 (350–200) кг. Основной недостаток вариационного размаха заключается в том, что он не отражает внутренних изменений признака и полностью зависит от отдельных случаев, оказывающихся на обоих полюсах ранжированного ряда. Поэтому вариационный размах используется для поверхностной характеристики вариации признака в статистической совокупности. В некоторых случаях для приближенной обобщающей характеристики вариации признака может быть рассчитано среднее линейное отклонение, которое выражается в простой и взвешенной формах. Поскольку математическая сумма линейных отклонений (Σ Простое среднее линейное отклонение, рассчитываемое для ранжированного ряда, находят следующим образом:
где Взвешенное среднее линейное отклонение, которое может быть найдено для дискретного или интервального ряда распределения, рассчитывают по формуле
где fх – частота вариационного признака. Как один из простейших показателей, оно находит ограниченное применение. Главным образом может быть использовано лишь для приближенной характеристики внутренних колебаний вариационного признака в статистической совокупности, поскольку оно рассчитывается с нарушением математических правил. Поэтому для более точной и объективной оценки внутренних изменений основными показателями вариации являются следующие: среднее квадратической отклонение и коэффициент вариации. Дисперсия как показатель колеблемости признака не играет какой-либо самостоятельной роли при оценке вариации признака в статистической совокупности. Вместе с тем дисперсия представляет особый интерес при рассмотрении и применении дисперсионного метода. простая – взвешенная – Дисперсия является промежуточной величиной в расчетах, не имеет экономического смысла и единиц измерения. Она является базой для расчета средней квадратической величины. Дисперсию можно рассчитать и более упрощенным способом:
Среднее квадратическое отклонение рассчитывается на базе средней квадратической величины. Оно выступает в невзвешенной (простой) и взвешенной формах. Для ранжированного ряда рассчитывают невзвешенное (простое) среднее квадратическое отклонение по следующей формуле:
где Взвешенное среднее квадратическое отклонение рассчитывают для дискретного или интервального ряда:
где fх – частота (веса) в вариационном ряду. Измеряется оно в тех же единицах, что и варианты изучаемого признака в статистической совокупности. Характеризует среднюю колеблемость вариант в этой совокупности и широко используется в качестве одного из наиболее точных и объективных показателей вариации не только в статистике, но и в технике, биологии, других отраслях знаний. Коэффициент вариации представляет собой относительный показатель, который можно рассчитать по формуле
где Vх – коэффициент вариации признака х в статистической совокупности;
Целесообразно обратить внимание на то, что базой (основанием) для расчёта коэффициента вариации может быть не только средняя величина, но и заменяющие её величины (например, мода и медиана). Коэффициент вариации, будучи относительной величиной, абстрагирует различия абсолютных показателей вариации разных признаков. Обычно его выражают в процентах и используют как объективную меру колеблемости вариант в статистической совокупности. В этом случае коэффициент вариации может характеризовать количественную однородность или разнородность изучаемых признаков в составе статистической совокупности. Если коэффициент вариации выше 10,0% (для малой статистической совокупности) или 33,3% (для большой статистической совокупности), то статистическая совокупность по заданному признаку считается неоднородной. Коэффициент вариации может быть использован при сравнении колеблемости нескольких признаков как в одной и той же статистической совокупности, так и в различных. Расчеты данных характеристик по взвешенной форме можно выполнить с помощью следующего макета (табл.8).
Т а б л и ц а 7.1. Вспомогательные расчеты для определения Дата добавления: 2016-06-06 | Просмотры: 543 | Нарушение авторских прав |
 (7.1)
(7.1) – соответственно конечная (максимальная) и начальная (минимальная) варианты.
– соответственно конечная (максимальная) и начальная (минимальная) варианты. ), согласно первому свойству средней арифметической величины, всегда равно нулю, то для расчета среднего линейного отклонения берут сумму линейных отклонений по модулю.
), согласно первому свойству средней арифметической величины, всегда равно нулю, то для расчета среднего линейного отклонения берут сумму линейных отклонений по модулю.
 (7.2)
(7.2) – среднее линейное отклонение;
– среднее линейное отклонение;  – линейное отклонение индивидуальных вариант от их среднего
– линейное отклонение индивидуальных вариант от их среднего  ; n – число вариант в статистической совокупности.
; n – число вариант в статистической совокупности. (7.3)
(7.3) ; (7.4)
; (7.4) . (7.5)
. (7.5)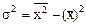 . (7.6)
. (7.6) (7.7)
(7.7) – среднее квадратическое отклонение вариационного признака; х – индивидуальные варианты в ранжированном ряду;
– среднее квадратическое отклонение вариационного признака; х – индивидуальные варианты в ранжированном ряду;  – среднее значение признака в статистической совокупности; n – число вариант в ряду.
– среднее значение признака в статистической совокупности; n – число вариант в ряду. (7.8)
(7.8) (7.10)
(7.10) – среднее квадратическое отклонение признака х;
– среднее квадратическое отклонение признака х;  – среднее значение признака в статистической совокупности.
– среднее значение признака в статистической совокупности.