 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Уравнение прямолинейной регрессииКорреляционную связь в форме, близкой к прямолинейной, можно представить в виде уравнения прямой линии:
где В уравнении 9.8 параметр Для нахождения параметров
При расчете искомых параметров
Т а б л и ц а 11.5. Вспомогательные расчеты для определения параметров уравнения прямолинейной связи
Таким образом, для решения системы нормальных уравнений (11.9 и 11.10) необходимо найти значения Σх, Σу, Σху и Σх2. Допустим, необходимо определить, как изменяется в среднем урожайность рапса в зависимости от колебания доз минеральных удобрений по данным статистической совокупности из 30 сельскохозяйственных организаций, если известно, что дозы удобрений колеблются в пределах от 56 до 183 кг действующего вещества на 1 га, а урожайность рапса – от 16,9 до 30,4 ц/га. Для составления уравнения прямолинейной регрессии (11.8) по имеющимся данным необходимо решить систему нормальных уравнений. С этой целью прежде всего составим рабочую табл. 11.6.
Т а б л и ц а 11.6. Вспомогательные расчеты для определения параметров уравнения прямолинейной взаимосвязи
Подставим полученные в табл. 11.6 конкретные значения Σх=3283, Σу=640, Σху=91204 и Σх2=535692 в уравнения 11.9 и 11.10; получим:
Для расчета коэффициента пропорциональности
Вычтем четвертое уравнение из третьего. Получим 21,3 – 27,7 = а+а+109,4в – 163,2 в; - 6,4 = - 53,8 в; в = 0,12. Теперь найдем параметр а, подставив значение в, например, в третье уравнение: 21,3 = а + 109,4. · 0,12; а=8,2. Уравнение прямолинейной регрессии, выражающее зависимость между дозами минеральных удобрений и урожайностью рапса, имеет следующий вид:
Коэффициент пропорциональности в показывает, что повышение доз внесения в почву минеральных удобрений на 1 кг действующего вещества может вызвать прирост урожайности рапса в сельскохозяйственных организациях 12 кг. Это свидетельствует о существенной роли минеральных туков в достижении высоких и устойчивых урожаев сельскохозяйственных культур.
Дата добавления: 2016-06-06 | Просмотры: 535 | Нарушение авторских прав |
 (11.8)
(11.8)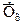 – среднее значение результативного признака; х – значение факторного признака;
– среднее значение результативного признака; х – значение факторного признака;  – параметр уравнения, обычно характеризующий минимальное значение результативного признака;
– параметр уравнения, обычно характеризующий минимальное значение результативного признака; 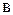 – коэффициент пропорциональности изменения признака-результата.
– коэффициент пропорциональности изменения признака-результата. характеризует среднее значение результативного признака у при элиминировании признака-фактора х, т.е. х=0. Коэффициент в зависимости от знака (+) или (–) показывает пропорциональность изменения результата у, т.е. его приращения или убывания при абсолютном изменении фактора на каждую его единицу.
характеризует среднее значение результативного признака у при элиминировании признака-фактора х, т.е. х=0. Коэффициент в зависимости от знака (+) или (–) показывает пропорциональность изменения результата у, т.е. его приращения или убывания при абсолютном изменении фактора на каждую его единицу.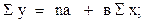 (11.9)
(11.9) (11.10)
(11.10)

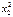



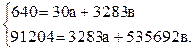
 разделим уравнения 1,2 на числа, находящиеся при
разделим уравнения 1,2 на числа, находящиеся при 
 (11.11)
(11.11)