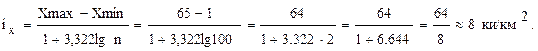АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Работников животноводства

Основное преимущество дискретного ряда заключается в его компактности по сравнению с ранжированным рядом. Дискретный ряд распределения разрабатывается в тех случаях, когда варьирующий признак принимает сравнительно небольшое число значений, т.е. встречается в ограниченном количестве вариант. В таких случаях имеется возможность охарактеризовать вариацию признака в статистической совокупности довольно подробно и точно.

Для графического изображения дискретного вариационного ряда в системе прямоугольных координат необходимо на оси абсцисс разместить независимую переменную – значения признака (варианты), а на оси ординат – локальные частоты ряда. Полученную геометрическую фигуру – многоугольник – принято называть полигоном распределения (рис. 3.2).

Рис. 3.2. Распределение средних перерабатывающих организаций АПК по численности работников (полигон распределения)

При достаточно большой статистической совокупности, которая может насчитывать, например, несколько сот единиц, обычно получаем одновершинный, близкий к симметричному, полигон распределения. Если же статистическая совокупность ограничена несколькими десятками единиц, то полигон может иметь многовершинную, как правило, асимметричную форму.

Это еще раз подтверждает, что статистические закономерности проявляются в условиях достаточно высокой представительности совокупности.

Во многих случаях, когда статистическая совокупность включает большое или тем более бесконечное число вариант, что чаще всего встречается при непрерывной вариации, практически невозможно и нецелесообразно формировать группу единиц для каждой варианты. В таких случаях объединение статистических единиц в группы возможно лишь на базе интервала, т.е. такой группы, которая имеет определенные пределы значений варьирующего признака. Они обозначаются двумя числами, указывающими верхнюю и нижнюю границы каждой группы. Применение интервалов приводит к формированию интервального ряда распределения.

Интервальный рад – это вариационный ряд, варианты которого представлены в виде интервалов. Он может формироваться с равными инеравными интервалами, при этом выбор принципа построения этого ряда зависит главным образом от степени представительности и однородности статистической совокупности. Если совокупность достаточно велика (представительна) по числу единиц и вполне однородна по своему составу, то в основу формирования интервального ряда целесообразно положить принцип равенства интервалов. Обычно по этому принципу образуют интервальный ряд по тем совокупностям, где размах вариации сравнительно невелик, т.е. максимальная и минимальная варианты различаются между собой обычно в несколько раз. При этом величина равных интервалов рассчитывается отношением размаха вариации признака к заданному числу образуемых интервалов. Для определения равного интервала может быть использована формула Стерджесса [4] (обычно при небольшой вариации интервальных признаков и большом числе единиц в статистической совокупности):

(3.2)

где i_X – величина равного интервала; х _max, х _min— максимальная и минимальная варианты в статистической совокупности; n— число единиц в совокупности.

Пример. Целесообразно рассчитать размер равного интервала по плотности радиоактивного загрязнения цезием - 137 в 100 населенных пунктах Краснопольского района Могилевской области, если известно, что начальная (минимальная) варианта равна 1ки/км², конечная ( максимальная) – 65 ки/км². Воспользовавшись формулой (3.2), получим:

Следовательно, при формировании интервального ряда с равными интервалами по плотности загрязнения цезием - 137 населенных пунктов Краснопольского района размер равного интервала может составить 8 ки/км².

В условиях неравномерного распределения, т.е. когда максимальная иминимальная варианты различаются в десятки или сотни раз, при формировании интервального ряда можно применить принцип неравных интервалов. Неравные интервалы обычно увеличиваются по мере перехода к большим значениям признака.

По форме интервалы могут быть закрытыми и открытыми. Закрытыми принято называть те, у которых обозначены нижняя и верхняя границы. Открытые имеют только одну границу: в первом интервале – верхняя, в последнем — нижняя граница.

Интервальные ряды, особенно с неравным интервалами, целесообразно оценивать с учетом плотности распределения, простейшим способом расчета которой является отношение локальной частоты (или частости) к размеру интервала. Для практического формирования интервального ряда можно воспользоваться макетом табл. 3.7.

Основное преимущество интервального ряда — его предельная компактность; в то же время в интервальном ряду распределения индивидуальные варианты признака скрыты в соответствующих интервалах.

При графическом изображении интервального ряда в системе прямоугольных координат на оси абсцисс откладывают нижние и верхние границы интервалов, на оси ординат – локальные частоты ряда.

Т а б л и ц а 3.7. Порядок формирования интервального ряда населённых пунктов Краснопольского района по плотности радиоактивного загрязнения цезием – 137

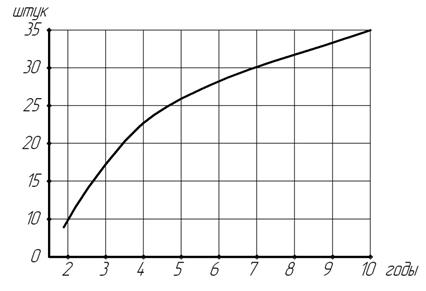
Графическое построение интервального ряда отличается от построения полигона распределения тем, что каждый интервал имеет нижнюю и верхнюю границы, а одному какому - либо значению ординаты соответствуют две абсциссы. Поэтому на графике интервального ряда отмечается не точка, как в полигоне, а линия, соединяющая две точки. Эти горизонтальные линии соединяются друг с другом вертикальными отрезками и получается фигура ступенчатого многоугольника, который принято называть гистограммой распределения (рис.3.3).

Рис. 3.3. Распределение работников по стажу в сельскохозяйственных организациях (гистограмма распределения)

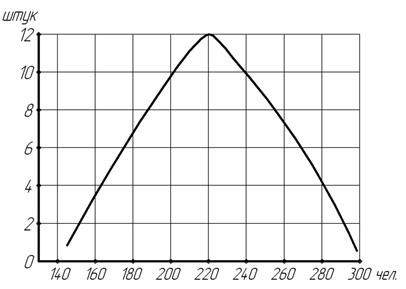
При графическом построении интервального ряда по достаточно большой статистической совокупности гистограмма приближается к симметричной форме распределения. В тех же случаях, где статистическая совокупность невелика, как правило, формируется асимметричная гистограмма.

В некоторых случаях целесообразно формировать ряд накопленных частот, т.е. кумулятивный. Его можно образовать на основе дискретного либо интервального ряда распределения. При графическом изображении кумулятивного ряда в системе прямоугольных координат на оси абсцисс откладывают варианты, на оси ординат — накопленные частоты (частости). Полученную при этом кривую линию принято называть кумулятой распределения (рис.3.4).

Рис. 3.4. Распределение тракторов по продолжительности эксплуатации в СПК «Нива» (кумулята распределения)

Формирование и графическое изображение различных видов вариационных рядов способствует упрощенному расчету основных статистических характеристик, помогает лучше понять сущность законов распределения статистической совокупности. Анализ вариационного ряда приобретает особенное значение в тех случаях, когда необходимо выявить и проследить зависимость между вариантами и частотами (частостями). Эта зависимость проявляется в том, что число случаев, приходящихся на каждую варианту, определенным образом связано с величиной этой варианты, т.е. с возрастанием значений варьирующего признака частоты (частости) систематически изменяются. Это означает, что числа в столбце частот (частостей) подвержены не хаотическим колебаниям, а изменяются в определенном направлении, порядке и последовательности.

Если в изменении частот обнаруживается некая систематичность, то это означает, что мы находимся на пути к выявлению закономерности. Система, порядок, последовательность в изменении частот – это отражение общих причин, условий, характерных для всей совокупности.

Не следует считать, что закономерность распределения всегда дается в готовом виде. Встречается довольно много вариационных рядов, в которых частоты причудливо скачут, то возрастая, то уменьшаясь. В таких случаях целесообразно выяснить, с каким распределением имеет дело исследователь: то ли этому распределению вовсе не свойственны закономерности, то ли его характер еще не выявлен. Первый случай встречается редко, второй– явление довольно частое и распространенное.

Так, при формировании интервального ряда общее число статистических единиц может быть небольшим, и в каждый интервал попадает малое число вариант (например, 1–3 единицы). В таких случаях рассчитывать на проявление какой-либо закономерности не приходится. Для того чтобы на основе случайных наблюдений получился закономерный результат, необходимо вступление в силу закона больших чисел, т.е. чтобы на каждый интервал приходилось не несколько, а десятки и сотни статистических единиц. С этой целью надо стараться, по возможности, увеличивать число наблюдений. Это самый верный способ обнаружения закономерности в массовых процессах. Если же не представляется реальная возможность увеличить число наблюдений, то выявить закономерность можно уменьшением числа интервалов в ряду распределения, тем самым достигается увеличение численности частот в каждом интервале. Это означает, что случайные колебания каждой статистической единицы накладываются друг на друга, "сглаживается", превращаясь в закономерность.

Формирование и построение вариационных рядов позволяет получить лишь общую, приближенную картину распределения статистической совокупности. Например, гистограмма лишь в грубой форме выражает зависимость между значениями признака и его частотами (частостями) Поэтому вариационные ряды по существу являются лишь основой для дальнейшего, углубленного изучения внутренней закономерности статического распределения.

Дата добавления: 2016-06-06 | Просмотры: 423 | Нарушение авторских прав