 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Способы аналитического выравнивания динамического рядовВыявить общую тенденцию развития уровней динамического ряда можно с помощью различных приемов аналитического выравнивания, наиболее часто осуществляемого следующими способами: во-первых, выравниванием по прямой линии; во- вторых, по показательной кривой; в-третьих, по гиперболе; в-четвертых, по параболе второго порядка. Способы аналитического выравнивания хотя и содержит в себе ряд условностей, но более совершенны по сравнению с рассмотренными выше приемами сглаживания уровней путем укрупнения периодов и скользящей средней. Аналитическое выравнивание облегчает выявление общей тенденции и изучение сезонных колебаний в характере динамического ряда. Выбор того иного способа аналитического выравнивания обусловлен характером (типом) динамики. Он может быть выражен в виде аналитических уравнений, которым на координатном графике соответствует определенная линия – прямая, гипербола, парабола и т.п. Тип динамики целесообразно учитывать при выборе способов аналитического выравнивания динамических рядов. В некоторых случаях фактический ряд динамики может характеризоваться значительными колебаниями уровней, причем положительные и отрицательные цепные абсолютные приросты примерно в равной мере отклоняются от средних значений. Если динамический ряд имеет более или менее стабильные абсолютные приросты, то выравниваемый динамический ряд может быть выражен в виде прямой линии. При этом на координатном графике фактический ряд динамики целесообразно показать прямолинейно. При выравнивании по прямой линии закономерно изменяющиеся уровни динамического ряда рассчитываются как функция времени, выражающаяся уравнением:
где Для расчета параметров уравнения прямой линии рекомендуется применять способ наименьших квадратов, основу которого составляет следующие требование: сумма квадратов отклонений фактических уровней ряда (У) от выровненных и лежащих на искомой линии теоретических уровней
Этому требованию удовлетворяет система нормальных уравнений, которые в соответствии с обозначениями формулы (10.20) могут быть записаны следующим образом:
где У – значения фактических уровней ряда динамики; t – порядковые номера периодов или моментов времени; n – число фактических уровней динамического ряда. Систему нормальных уравнений (10.22 и 10.23) можно упростить, если срединный уровень ряда условно принять на начальный. В этом случае Σt=0, а система уравнений примет следующий вид:
откуда параметры а, в можно выразить так:
Определив параметры а, в, легко найти выравненные значения уровней Например, необходимо выровнять по прямой линии динамический ряд, характеризующий реализацию скота (ж.м.) откормочным комплексом «Сож» (табл. 9.9). В этой же таблице приводится и порядок определения искомых значений ΣУ, ΣУt, Σt2, которые помогут найти параметры а, в уравнения (9.20).
Т а б л и ц а 9.9. Аналитическое выравнивание реализации скота Дата добавления: 2016-06-06 | Просмотры: 581 | Нарушение авторских прав |
 (9.20)
(9.20) – выровненные значения уровней ряда; t – периоды или моменты времени, к которым относятся уровни; а, в – параметры уравнения (искомой прямой).
– выровненные значения уровней ряда; t – периоды или моменты времени, к которым относятся уровни; а, в – параметры уравнения (искомой прямой). должна иметь минимальное значение, т.е.
должна иметь минимальное значение, т.е. (9.21)
(9.21)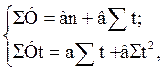
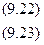

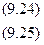
 (9.26)
(9.26) (9.27)
(9.27) и изобразить их графически в виде теоретической прямой линии.
и изобразить их графически в виде теоретической прямой линии.