 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Показатели тесноты корреляционных связей. Корреляционное отношениеОдним из центральных вопросов, решаемых с помощью корреляционного метода, является определение и оценка количественной меры тесноты связи между факторными и результативными признаками. При решении однофакторного или многофакторного корреляционного комплекса универсальным показателем тесноты взаимосвязи между изучаемыми признаками считается корреляционное отношение, позволяющее довольно точно измерить и оценить влияние факторных признаков на признаки- результаты при любой форме корреляционной зависимости. Корреляционное отношение –– показатель, который можно рассчитать для простой или множественной корреляции на базе данных, получаемых в процессе решения дисперсионного комплекса:
где Wф — объем систематической (факторной) вариации; Wобщ — объем общей вариации признака-результата. Корреляционное отношение может обеспечить довольно высокий уровень точности количественного измерения тесноты взаимосвязи между изучаемыми признаками, так как оно позволяет полнее «уловить» все колебания, вызванные влиянием факторных признаков на результат. Вместе с этим преимуществом корреляционное отношение содержит существенный недостаток: имея всегда положительное значение, при обратной корреляционной зависимости оно не показывает направление связи между изучаемыми признаками. Поэтому для выявления направленности корреляционной зависимости между признаками-факторами и признаками-результатами нередко приходится использовать графический прием. При корреляционных связях обычно изучаются взаимоотношения разноименных величин. Поэтому приходится сопоставлять не линейные отклонения индивидуальных вариант, а их преобразованные значения, нередко выраженные в отвлеченных числах. Дата добавления: 2016-06-06 | Просмотры: 2175 | Нарушение авторских прав |
, (11.1)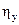
- корреляционное отношение;