 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Аналитическое выравнивание по показательной кривойВ некоторых случаях, например, в процессе ввода в действие и освоения новых производственных мощностей, для динамического ряда может быть характерно быстрорастущее изменение уровней, т.е. цепные темпы роста уровней могут существенно повышаться. При графическом изображении такого ряда эмпирическая линия по форме приближается к экспоненте (показательной кривой). С учетом этих и других особенностей характера динамики аналитическое выравнивание уровней, т.е. расчет их теоретических значений, может быть проведен путем применения способа показательной кривой. Онавыражается следующим уравнением:
где: Это выражение путем логарифмирования можно превратить в уравнение прямой линии: Поскольку в уравнении прямой линии (9.20) параметр Например, необходимо выравнять динамический ряд производства яиц на птицефабрике за 2006 – 2010 гг. по способу показательной кривой. Вспомогательные расчеты по выравниванию ряда приведены в табл. 9.10. Значения параметров уравнения показательной кривой определим следующим образом:
Следовательно, уравнение показателей кривой, характеризующей общую тенденцию уровней выровненного динамического ряда, можно представить в виде:
Т а б л и ц а 9.10. Аналитическое выравнивание производства яиц На птицефабрике
Подставляя в это уравнение значение отклонений t и логарифмируя его, нетрудно определить уровни выравненного ряда динамики производства яиц на птицефабрике; например, Аналитическое выравнивание по показательной кривой может найти широкое применение при статистическом прогнозировании многих показателей.
Дата добавления: 2016-06-06 | Просмотры: 557 | Нарушение авторских прав |
 (9.29)
(9.29) – выровненное значение уровня динамического ряда; а, в – параметры уравнения; t – отклонения порядкового номера уровня от срединного номера.
– выровненное значение уровня динамического ряда; а, в – параметры уравнения; t – отклонения порядкового номера уровня от срединного номера.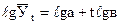 .
. а параметр
а параметр  то соответственно этому
то соответственно этому 
 Если рассчитать значения логарифмов, то нетрудно найти параметры уравнения показательной кривой.
Если рассчитать значения логарифмов, то нетрудно найти параметры уравнения показательной кривой.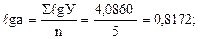

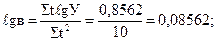
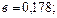
 (9.30)
(9.30)
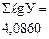
 gУ
gУ
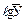

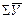 =34,2
=34,2
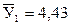 млн. шт.;
млн. шт.;  млн. шт. и т.д.
млн. шт. и т.д.