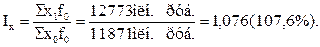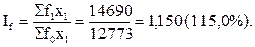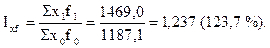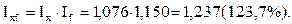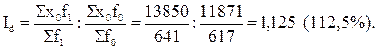|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Индексы постоянного и переменного состава
Статистические индексы, рассчитываемые с весами или соизмерителями на уровне какого-либо одного периода и показывающие изменение только индексируемой величины, принято называть индексами постоянного (фиксированного) состава. Они могут выражаться в двух вариантах. Во-первых, веса (соизмерители) фиксируются на уровне базисного периода. Тогда индекс постоянного состава в общем виде можно представить следующим образом:
где х1, х0 – индексируемый показатель в отчетном и базисном периодах; f0 – веса (соизмерители) базисного периода. Во-вторых, веса (соизмерители) фиксируют на уровне отчетного периода. В соответствии с этим вариантом общий индекс постоянного состава можно выразить формулой
где f1 – веса (соизмерители) отчетного периода. Совершенно очевидно, что применение различной системы весов в формулах индексов постоянного состава приводит к различной количественной оценке роли факторов в формировании общего результативного показателя. В связи с этим в основу построения общих индексов постоянного состава необходимо вкладывать экономический смысл индексируемых показателей. Считается целесообразным, что при индексировании количественных признаков за веса (соизмерители) необходимо брать показатели базисного, при индексировании качественных признаков – веса (соизмерители) отчетного периода. Неслучайно поэтому при индексировании количества товара используют соизмерители (цены) обычно базисного периода, а при индексировании цен – веса (количество товара) отчетного периода. Статистические индексы, выражающие соотношение средних уровней изучаемого явления, относящиеся к разным периодам времени или разным территориям, называют индексами переменного состава. Характерная особенность этих индексов, отличающая их от индексов постоянного состава, состоит в том, что индексы переменного состава выражают изменение не только индексируемой величины, но и весов (соизмерителей). Если необходимо показать изменение среднего значения индексируемого признака за два, три и более периодов, то индекс переменного состава можно выразить следующем образом:
Необходимо обратить внимание на то, что в формуле (10.7) отношения В сельскохозяйственной сфере АПК индексы постоянного и переменного состава могут применяться при проведении факторного анализа изменений в валовом сборе продукции сельскохозяйственных культур, валовом производстве продукции животноводства, стоимости валовой и товарной продукции, затратах труда, его производительности и оплаты, себестоимости продукции и т.д. Формирование сложных статистических показателей во времени и пространстве неизбежно связано со структурными изменениями их составных частей. В связи с этим для измерения степени влияния структурных сдвигов на изменение сложных показателей можно воспользоваться формулой индекса структуры:
Общие индексы структурных изменений могут применяться при углубленном факторном анализе многих сложных показателей, характеризующих результаты работы АПК: стоимости валовой, товарной продукции, валового дохода (добавленной стоимости), производственных затрат, себестоимости продукции, прибыли, убытков и т.д. Общие индексы постоянного и переменного состава, а также структурных сдвигов рассчитаем на примере динамики денежной выручки от реализации продукции льноперерабатывающей организации «Двина». С этой целью приведем вспомогательные показатели (табл. 10.2).
Т а б л и ц а 10.2 Вспомогательные расчеты для определения индексов постоянного и переменного состава в льноперерабатывающей организации «Двина»
Прежде всего определим общий индекс количества льноволокна, произведенного в перерабатывающей организации «Двина» за отчетный период по сравнению с базисным, т.е. индекс постоянного состава, в котором соизмерители (цены) фиксируются на уровне базисного периода (10.5):
Общий индекс цен на произведенную продукцию в отчетном периоде, в котором веса (количество продукции) фиксируются на уровне отчетного периода (индекс постоянного состава) рассчитываем так:
Общее изменение выручки от реализации всего льноволокна в перерабатывающей организации «Двина» за отчетный период по сравнению с базисным рассчитаем следующим образом:
Этот же результат можно получить, если представить общий индекс денежной выручки как произведение индекса количества продукции и индекса цен:
Таким образом, с помощью индексного приема выявлено, что общий объем денежной выручки от реализации льноволокна в перерабатывающей организации «Двина» за отчетный период по сравнению с базисным возрос в 1,237 раза, или на 23,7 %. За счет увеличения количества реализованной продукции выручка повысилась в 1,076 раза (на 7,6 %), а за счет повышения цен на льноволокно – в 1,15 раза (на 15 %). Средневзвешенный индекс цен на льноволокно перерабатывающей организации (индекс переменного состава) рассчитаем следующим образом:
Полученный результат указывает на то, что в отчетном периоде по сравнению с базисным средняя цена на льноволокно перерабатывающей организации повысилась в 1,193 раза, или на 19,3 %. Изменения объема денежной выручки, вызванные структурными сдвигами в количестве реализованного льноволокна за отчетный период по сравнению с базисным, можно рассчитать по формуле индекса структуры (10.8):
Результат показывает, что в льноперерабатывающей организации «Двина» за отчетный период по сравнению с базисным произошли структурные изменения в объеме реализованного льноволокна: повысилась доля более высоких, т.е. ценных номеров продукции. Это способствовало не только росту средних цен, но и увеличению денежной выручки от реализации льноволокна в 1,125 раза (на 12,5 %).
Дата добавления: 2016-06-06 | Просмотры: 841 | Нарушение авторских прав |
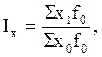 (10.5)
(10.5) (10.6)
(10.6) (10.7)
(10.7) и
и  представляют собой средневзвешенный индексируемый показатель соответственно в отчетном и базисном периодах. Поэтому индексы переменного состава иногда называют индексами средних показателей.
представляют собой средневзвешенный индексируемый показатель соответственно в отчетном и базисном периодах. Поэтому индексы переменного состава иногда называют индексами средних показателей.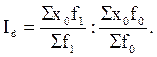 (10.8)
(10.8)