 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
СОСУДИСТЫЕ ЗАБОЛЕВАНИЯ ГОЛОВНОГО МОЗГА. Гильом Франсуа де Лопиталь (1661-1704) – французский математикГильом Франсуа де Лопиталь (1661-1704) – французский математик. При вычислении пределов, как известно, приходится раскрывать неопределенности разных видов. В этом параграфе мы познакомимся с правилом Лопиталя раскрытия неопределенностей вида Теорема 1. Пусть функции
Доказательство. Рассмотрим интервал Заметим, что мы рассмотрели случай Аналогично рассматривается интервал В теореме 1 Теорема 2. Пусть функции
Доказательство. Положим Для случая неопределенности вида Теорема 3. Пусть функции
Без доказательства. Замечания. 1) Теоремы 1, 2, 3 справедливы во всех случаях, когда 2) Теоремы 1, 2, 3 называют правилом Лопиталя раскрытия неопределенностей. 3) Если при вычислении предела по правилу Лопиталя снова получается неопределенность вила 4) Применение правила Лопиталя целесообразно комбинировать с известными из главы I способами раскрытия неопределенностей. В этом случае результат получается быстрее. 5) Неопределенности вида Примеры. 1) Для
функция Поскольку при 2) Для Таким образом, показательная функция растет быстрее, а логарифмическая функция медленнее, чем степенная. 3)
СОСУДИСТЫЕ ЗАБОЛЕВАНИЯ ГОЛОВНОГО МОЗГА _____ Часть 1 (этиопатогенез, клиника) Дата добавления: 2015-01-18 | Просмотры: 927 | Нарушение авторских прав |
 и
и  .
.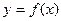 и
и  непрерывны в точке
непрерывны в точке  , дифференцируемы в некоторой проколотой окрестности
, дифференцируемы в некоторой проколотой окрестности  точки
точки 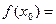
 . Пусть, кроме того,
. Пусть, кроме того,  для всех
для всех  . Тогда, если существует
. Тогда, если существует  , то существует и
, то существует и  , причем
, причем − правую половину окрестности
− правую половину окрестности  . Заметим, что на отрезке
. Заметим, что на отрезке  к функциям
к функциям  и
и  можно применить теорему Коши (
можно применить теорему Коши (
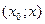 ). По теореме Коши существует точка
). По теореме Коши существует точка  такая, что
такая, что 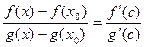 или, так как
или, так как  ,
, 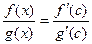 . Если
. Если  , то, очевидно, и
, то, очевидно, и  . По условию теоремы
. По условию теоремы 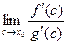 существует, поэтому существует и
существует, поэтому существует и  , т.е. в последних пределах
, т.е. в последних пределах  . Тем самым равенство (7.1) и теорема доказаны.
. Тем самым равенство (7.1) и теорема доказаны. .
. , причем
, причем  , и пусть
, и пусть  . Тогда, если существует
. Тогда, если существует 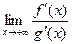 , то существует и
, то существует и  , причем
, причем ,
, 
 ,
, 
 . Тогда функции
. Тогда функции  и
и  непрерывны в точке
непрерывны в точке 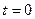 справа. Кроме того,
справа. Кроме того, 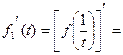
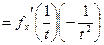 ,
, 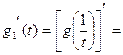
 , т.е. функции
, т.е. функции  , причем
, причем  . Поэтому
. Поэтому  =│теорема 1│=
=│теорема 1│= 
 . Тогда, если существует
. Тогда, если существует 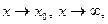
 , а
, а  конечен или бесконечен.
конечен или бесконечен. можно преобразовать к виду
можно преобразовать к виду  имеем
имеем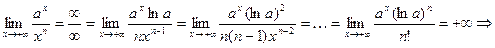
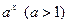 – бесконечно большая более высокого порядка при
– бесконечно большая более высокого порядка при  , чем
, чем  при любом натуральном значении n.
при любом натуральном значении n. , то
, то  и это утверждение остается справедливым для
и это утверждение остается справедливым для  , где
, где  – любое число.
– любое число. – бесконечно большая более высокого порядка при
– бесконечно большая более высокого порядка при  .
.
 .
.