АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Приложение 2. Определение продолжительности проходимости протеза, артерий или шунтов

Несмотря на некоторые неточности, life table метод (LT) — анализ таблиц жизни — является одним из лучших и самым ис­пользуемым способом вычисления про­ходимости протезов у пациентов после

реваскуляризации в различные временные отрезки и сроки наблюдения. Равнознач­ным методом является анализ выживае­мости Kaplan—Meier (KM). Ниже описы­ваются и сравниваются обе методики.

Лучше всего охарактеризовали метод анализа таблиц жизни Peto и соавт. в двух статьях "British Journal of Cancer" в 1976 и 1977 гг., но ранее подобный метод опи-

сывался Berkson и Cage в 1950 г., Cutler и Ederer в 1958 г. В методе есть две черты, которые характеризуют оперативное вмешательство. Первая — та, что откла­дывается на кривой выживаемости — на­пример, случаи тромбозов протеза, кото­рые группируются по временным интер­валам. После этого вычисляются уровни выживаемости для каждого интервала и используются для вычисления кумуля­тивной проходимости, объясняющей по­лученную кривую. Вторая важная черта — допущение, что те пациенты, которые "теряются" в отдаленном периоде наблю­дения в определенном интервале (так на­зываемые сенсорные данные), рассмат­риваются как выбывшие в середине ин­тервала. Благодаря этому допущению выполняется характерная для методики анализа таблиц жизни коррекция вычис­ленного уровня тромбозов в данном ин­тервале:

Эта коррекция предполагает, что вы­бывшие индивидуумы пополняют группу риска только до середины интервала. Вышеприведенная формула математи­чески эквивалентна возрастанию уровня тромбозов на число ожидаемых тромбо­зов у половины из выбывшей группы:

Следующее последствие такого допу­щения для сенсорных данных или вы­бывших — уровень тромбозов принимает­ся одинаковым для всего интервала. Поэ­тому не является строго необходимым поступенчатое отображение графика таб­лиц жизни, так как кумулятивная прохо­димость — это результирующая условной вероятности в конце интервала, основан­ная на уровне тромбозов для всего интер­вала. График может быть представлен как прямые отрезки, соединяющие точки между рассчитанными уровнями прохо­димости в конце каждого интервала. При таком виде графика отрезки между ко­нечными точками интервалов не содер­жат случаев тромбоза протеза.

Анализ таблиц жизни должен вклю­чать следующие колонки в таблице (даны в алфавитном порядке): А — интервалы в 1 мес; В — количество протезов в груп­пе риска на момент начала наблюдения; С — количество тромбозов в течение ин­тервала; D — количество пациентов, вы­бывших из наблюдения в результате смерти, потерянных из виду или у кото­рых закончился период наблюдения в те­чение данного временного интервала (последние 3 колонки в дальнейшем ис­пользуют для вычислений); Е — уровень тромбозов в течение интервала; F — ку­мулятивная проходимость шунтов (в бо­лее общем плане — выживаемость); G — стандартная ошибка, %. Кумулятивный уровень смертности не является обяза­тельной частью таблицы LT.

Ниже приведены в наиболее простом виде вычисления для каждой колонки на основании приведенного в таблице при­мера. Интервал в месяцах (А) может быть выбран любой, меньший длительности

всего периода наблюдения, интервалы необязательно должны быть равными. Первым полезно обозначить временной интервал от 0 до 1 мес для оценки ранних тромбозов; следующий наиболее часто применяемый интервал — от 3 до 6 мес. Меньшие интервалы означают большую точность оценки. Количество протезов в группе риска в начале исследования в первом временном интервале (В) — ко­личество шунтов, включенных в исследо­вание, количество протезов в следующих колонках получается вычитанием коло­нок С и D из В. Количество выбывших из исследования (С): пациенты с проходи­мыми протезами в предыдущих времен­ных интервалах, которые погибли или потеряны для наблюдения в течение дан­ного временного интервала. Проходи­мость шунтов в данном временном ин­тервале (Е) равна "1 -уровень тромбозов в данном интервале", который в свою оче­редь вычисляется делением колонки С на колонку В минус половину колонки D, согласно приведенным выше теоретичес­ким соображениям. Кумулятивная про­ходимость (F) равна 100 % в первом вре­менном интервале, для каждого после­дующего интервала она вычисляется ум­ножением уровня проходимости для данного интервала на предыдущую куму­лятивную проходимость. Стандартная ошибка (G), % равна 100 х F х квадрат­ный корень из (1-F)/B, где F равно ку­мулятивной проходимости и В — коли­чество протезов в группе риска в начале интервала.

Примерно равноценный альтернатив­ный метод оценки проходимости — вы-

живаемость Kaplan—Meier (KM), кото­рый также называется product-limit. В этой методике данные не группируются по временным интервалам. События на кривой выживаемости отражают тромбоз каждого протеза. Никаких допущений об уровне тромбозов у выбывших больных не делается. В противоположность мето­ду таблиц жизни кривая выживаемости выглядит ступенчато, так в промежутки между событиями ничего не известно об уровне тромбозов. Можно рассматривать метод Kaplan—Meier как метод анализа таблиц жизни с маленькими интервала­ми, каждый из которых содержит одно событие. Те же данные, что и в примере первой методики, отражены в табл. 6.5 и графике Kaplan—Meier.

Метод анализа таблиц жизни позволя­ет оперировать большими группами дан­ных, что и является главным аргументом в пользу использования этой методики. Однако исследования проходимости шун­тов чаще не имеют дело с такими боль­шими группами данных и к тому же с внедрением компьютеров это неудобс­тво легко преодолимо. Анализ таблиц жизни нельзя использовать для группы, меньшей 30, тогда как метод Kaplan-Meier применим к любому количеству. Обе методики допустимы, если правиль­но используются и документируются. Данные на графиках 1 и 2 сравнивались между собой и в каждом случае поздние уровни проходимости были эквивалент­ны (рис. 6.14; 6.15).

Полные данные при использовании той или иной методики должны быть сведены в таблицы в каждой научной ра-

Таблица 6.5. Пример анализа выживаемости Kaplan—Meier

Условные обозначения (A—G) те же, что в табл. 6.4. Конечные точки исследования — те же.

5 - 4886

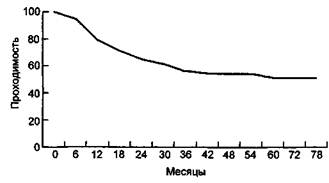
Рис. 6.14. Кривая прохо­димости. Анализ таблиц жизни.

боте с целью возможности проверки дан­ных, даже если редактор настаивает на публикации только графиков. Количест­во пациентов в группе риска в начале каждого интервала (периодически для Kaplan—Meier анализа) или стандартная ошибка для каждого вычисленного пока­зателя проходимости должны быть отоб­ражены при помощи "столбиковой" диа­граммы. При сравнении множественных кривых или графиков эти "столбики" мо­гут накладываться на кривую. Располагая столбики в противоположном графику направлении или используя выбранные интервалы вместо всех, можно избежать этого. Если рассчитанная стандартная ошибка проходимости превышает 10 %, кривая либо не должна отображаться, ли­бо должна быть представлена как преры­вистая линия, что означает ненадежность оценки. Сравнение кривых проходимос­ти (выживаемости) производится с помо­щью лог-ранк-теста.

Когда это возможно, отдельные расче­ты анализа таблиц жизни метода должны производится для каждого этапа опера­тивного вмешательства. В общем не ре­комендуется смешивать данные об опера­циях на различных уровнях инфраингви-

нальных артерий, а, например, опублико­вывать результаты бедренно-подколенно-го выше щели, ниже щели и бедренно-берцовые шунтирования раздельно. Ког­да это можно, особенно если делается вывод о существовании различий, долж­ны опубликовываться отдельные графи­ки и диаграммы результатов операций, выполняемых по разным показаниям (перемежающаяся хромота и критичес­кая ишемия), с различными путями от­тока, факторами риска и лечения, кото­рые влияют на проходимость (например, с дезагрегантами и без них, с диабетом и без него), тем более при попытках вы­явить различия между группами боль­ных. В некоторых случаях взаимозави­симость переменных будет ограничивать значимость выводов о различиях в этих подгруппах. В таких ситуациях жела­тельно применять регрессионный ана­лиз Сох.

Часто авторы, сообщающие о реваску-ляризациях, не публикуют данные о тром­бозах в ближайшем периоде, а затем ис­ключают эти случаи из дальнейшего ана­лиза кумулятивной проходимости. К при­меру, если тромбоз в ближайшем периоде наступает в 25 % случаев, а затем в тече-

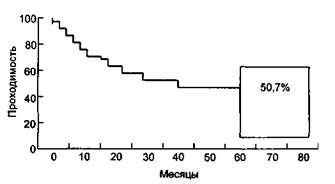
Рис. 6.15. Кривая прохо­димости Kaplan—Meier (данные см. в табл. 64).

ние отдаленного периода наблюдения 80 % шунтов проходимы, то кумулятив­ная проходимость у первично опериро­ванных больных составляет только 60 %. Подобно этому, при том же уровне бли­жайших тромбозов, если ²/₃ шунтов оста­ются проходимы, кумулятивная прохо­димость составляет меньше 50 %.

Дата добавления: 2015-02-06 | Просмотры: 1221 | Нарушение авторских прав