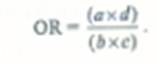АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Вероятность и шансы

Вероятность, используемая для выражения различных показателей, со­ответствует доле лиц обладающих некоторой характеристикой в опреде­ленной группе, например, возникновением болезни. При этом вероятность отсутствия той же самой характеристики может быть рассчитана путем вы­читания предыдущей вероятности из единицы (вероятность отсутствия со­бытия =1 — вероятность события). В свою очередь шансы — это отношение этих двух вероятностей (отношение вероятности того, что событие про­изойдет к вероятности того, что оно'не произойдет). Шансы и вероятность отражают одну и ту же информацию, но по-разному ее выражают. Одно может быть легко преобразовано в другое с помощью двух простых формул:

Шансы события = (вероятность события) / (1 — вероятность события),

Вероятность события = (шансы события) /1 + шансы события. Формула расчета отношения шансов для таблицы «2x2»:

Отношение шансов оценивают так же, как и относительный риск.

Величина отношения шансов равной единицы (ОR= 1) указывает на от­сутствие причинно-следственной связи изучаемого фактора и болезни.

Если отношение шансов меньше единицы (ОR. < 1) возможно предпо­ложение о защитных свойствах изучаемого фактора.

Величина ОR > 1 указывает на возможную связь между болезнью и па­губным действием изучаемого фактора.

В когортных исследованиях показатель отношение шансов — альтер­натива относительному риску. Поэтому допустимо их равноценное ис­пользование.

Следующий обязательный этап статистической обработки в когор­тных исследований — оценка достоверности различий. Для этого рас­считывают доверительные интервалы для показателей инцидентности, абсолютного риска, относительного риска, отношения шансов. Могут быть использованы критерий Пирсона (хи-квадрат) или точный крите­рий Фишера.

Дата добавления: 2015-02-05 | Просмотры: 1018 | Нарушение авторских прав